ANNEAUX COMMUTATIFS

ANNEAUX COMMUTATIFS

Dans tout ce qui suit, on se bornera à considérer des anneaux commutatifs unitaires, c’est-à-dire possédant un élément unité pour la multiplication, noté 1. Les définitions sont celles de l’article suivant, ANNEAUX ET ALGÈBRES.

De nombreux cas particuliers d’anneaux commutatifs unitaires ont été étudiés au XIX^e siècle, principalement à propos de recherches de théorie des nombres et de géométrie algébrique. Introduits à l’origine pour étudier la divisibilité dans de tels anneaux, les idéaux, cas particuliers de modules, se sont révélés essentiels dans de nombreuses questions. En fait, la classification des différents types d’anneaux s’effectue suivant la structure de leurs idéaux.

L’arithmétique des anneaux dits principaux est analogue à l’arithmétique des nombres entiers ou des polynômes; plus généralement, on peut étudier de manière satisfaisante l’arithmétique des anneaux de Dedekind : ici, les propriétés de divisibilité, déroutantes a priori, s’expriment harmonieusement dans le cadre de la théorie des idéaux. Une autre généralisation possible des anneaux principaux, qui englobe d’ailleurs la précédente, est liée à des conditions de finitude: tout idéal d’un anneau principal est formé des multiples d’un élément; plus généralement, on peut considérer les anneaux dans lesquels tout idéal est formé des combinaisons linéaires (à coefficients dans l’anneau) d’un nombre fini d’éléments, et ces anneaux, appelés noethériens , possèdent une remarquable propriété de stabilité, découverte par Hilbert, à savoir que l’anneau des polynômes sur un anneau noethérien est lui-même noethérien. Pour terminer, mentionnons ici la classe importante des anneaux locaux , qui possèdent un unique idéal maximal: cela signifie qu’il existe un idéal propre contenant tous les autres idéaux propres de l’anneau; ces anneaux jouent un grand rôle dans la théorie des variétés algébriques, différentiables ou analytiques, car les anneaux de germes de fonctions sont de ce type. L’étude des anneaux locaux est très liée à des considérations topologiques; nous renvoyons à ce propos aux articles algèbre TOPOLOGIQUE et théorie des NOMBRES – Nombres p -adiques.

Le tableau ci-dessus précise les rapports entre ces différents anneaux, chaque flèche exprimant qu’une propriété en entraîne une autre.

1. Notions fondamentales

Divisibilité

La présence dans un anneau de diviseurs de zéro, c’est-à-dire d’éléments a et b , tous deux non nuls, dont le produit est nul, rend illusoire toute théorie satisfaisante de la divisibilité. Les anneaux commutatifs sans diviseurs de zéro sont appelés des anneaux intègres ou anneaux d’intégrité . Nous allons, dans ce qui suit, préciser quelques propriétés de la divisibilité dans un tel anneau d’intégrité A. Dans toutes ces questions de divisibilité, seul intervient le fait que l’ensemble A des éléments non nuls de l’anneau A est muni d’une loi de composition interne x , y 轢 xy (la multiplication) associative, commutative, avec un élément unité ; un ensemble muni d’une loi possédant ces propriétés est appelé un monoïde . Nous énoncerons les définitions générales relatives à la divisibilité dans le cadre d’un monoïde A quelconque, ce qui sera utile dans la troisième partie.

On dit qu’un élément b de A divise un élément a de A, ou encore que a est divisible par b s’il existe un élément c tel que a = bc . Il est clair que cette notion de divisibilité généralise la notion usuelle de divisibilité dans le monoïde Z des entiers relatifs non nuls et possède des propriétés analogues: par exemple, si c divise b et si b divise a , alors c divise a .

Dans toutes les questions de divisibilité, un rôle essentiel est joué par les unités , qui sont les éléments inversibles (ou encore, avec la terminologie ci-dessus, les éléments qui divisent l’élément unité 1); si A est le monoïde des éléments non nuls d’un anneau d’intégrité A, ces éléments sont aussi appelés les unités de l’anneau: par exemple, dans l’anneau Z des entiers relatifs, les seules unités sont les nombres + 1 et 漣 1 et, dans l’anneau des polynômes à coefficients dans un corps K, ce sont les polynômes constants non nuls. Dans tous les cas, on vérifie facilement que les unités forment un groupe multiplicatif; pour un anneau A, la structure de ce groupe est une importante caractéristique arithmétique de A. Deux éléments a et b , qui diffèrent seulement par un élément inversible, c’est-à-dire tels que a = ub , u inversible, possèdent des propriétés de divisibilité très analogues et sont dits associés . Pour terminer ces définitions, indiquons qu’un élément a de A est dit premier , ou irréductible , s’il n’est pas inversible et si pour toute décomposition a = bc ; b , c éléments de A, l’un des deux facteurs b ou c est inversible. Un des problèmes fondamentaux de la divisibilité dans A est l’étude de la décomposition éventuelle de tout élément comme produit d’éléments premiers.

Corps des fractions d’un anneau d’intégrité

La construction du corps Q des nombres rationnels à partir de l’anneau Z des entiers relatifs se généralise sans difficulté à un anneau d’intégrité quelconque. Plus précisément, on a le résultat suivant: «Si A est un anneau d’intégrité, il existe un corps K contenant A comme sous-anneau et dont tous les éléments sont de la forme xy ^-1, x , y éléments de A. De plus, un tel corps K est unique à un isomorphisme laissant A fixe près.»

Pour faire comprendre la démonstration, analysons ce qu’est un nombre rationnel. Un nombre rationnel u est «défini» par une fraction p /q , où p et q sont des entiers relatifs, mais deux fractions p /q et p /q , distinctes, possédant des numérateurs et des dénominateurs distincts, peuvent définir le même nombre rationnel si pq = p q . De plus, si p /q et p /q sont des fractions définissant des nombres rationnels u et v , les fractions (pq +p q )/qq et pp /qq définissent les nombres rationnels u +v et uv . La démonstration générale est calquée sur la construction ci-dessus; donnons-en l’esquisse.

Nous allons d’abord définir la notion de «fraction». Pour cela, désignons par A l’ensemble des éléments non nuls de A et considérons l’ensemble A 憐 A des couples (x , y ), y 0; un tel élément (y , x ) s’appelle une «fraction» de numérateur x et de dénominateur y . Nous allons maintenant identifier des fractions (x , y ) et (x , y ) telles que xy = x y , c’est-à-dire considérer sur l’ensemble A 憐 A la relation d’équivalence ainsi définie. L’ensemble des classes d’équivalence forme un ensemble que nous désignerons par K. On vérifie alors facilement que, si on définit la somme et le produit de deux «fractions» par les formules:

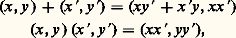on obtient sur K, par passage au quotient , deux opérations qui en font un corps; cela signifie que, si u et u sont des éléments de K représentés par des «fractions» (x , y ) et (x , y ), alors par définition, u +u et uu sont les éléments de K représentés par les «fractions» (x , y ) + (x , y ) et (x , y ) (x , y ) et que u + u et uu ainsi définis dont indépendants du choix des «fractions» représentant u et v .

Le plongement de A dans K s’effectue maintenant en identifiant tout élément de A à l’élément de K défini par la «fraction» (a , 1), dont le numérateur est égal à a et le dénominateur à 1. Remarquons que, si on identifie deux éléments a et b de A à leur image dans K, l’élément de K représenté par la «fraction» (a , b ) est bien le quotient (dans K) de a par b .

Le corps K que nous venons de construire s’appelle le corps des fractions de l’anneau A.

Idéaux

Rappelons qu’un idéal d’un anneau A est un sous-groupe additif qui est stable par multiplication par un élément quelconque de A, qu’il possède certaines propriétés ^{[cf. ANNEAUX ET ALGÈBRES]}. Nous nous contenterons de montrer comment on peut étendre aux idéaux le langage arithmétique usuel relatif aux nombres entiers.

Les idéaux du type le plus simple sont obtenus ainsi: si a est un élément d’un anneau A, l’ensemble des multiples de a , c’est-à-dire l’ensemble des éléments de la forme xa pour x parcourant A, est un idéal de A, noté (a ), et appelé l’idéal principal engendré par a . Un tel idéal est propre c’est-à-dire non réduit à 0 et différent de A tout entier si, et seulement si, a est non nul et non inversible. On verra, dans la deuxième partie, que tout idéal de l’anneau Z des entiers relatifs est de ce type. Remarquons au passage que, dans un anneau d’intégrité, deux éléments a et b non nuls engendrent le même idéal principal si et seulement s’ils sont associés, c’est-à-dire si b = ua , u inversible dans l’anneau: en effet, si (a ) = (b ), il existe des éléments u et v tels que b = ua , a = vb , d’où vua = a ; si a 0, on a donc vu = 1 puisqu’il n’y a pas de diviseurs de zéro dans l’anneau et ainsi u est inversible. Plus généralement, si a ¹, ..., a ⁿ sont des éléments de A, l’ensemble, noté (a ¹, ..., a ⁿ ) des éléments de la forme x ¹a ¹ + ... + x ⁿ a ⁿ pour x ¹ ..., x ⁿ parcourant A indépendamment l’un et l’autre est un idéal; la quatrième partie est consacrée à l’étude des anneaux dans lesquels tout idéal est de ce type.

Étant donné deux idéaux face=F9828 a et face=F9828 b, leur intersection face=F9828 a 惡 face=F9828 b est encore un idéal. Généralisons aux idéaux la notion de produit: face=F9828 a et face=F9828 b étant deux idéaux, l’ensemble des sommes finies a ¹b ¹ + ... + a ⁿ b ⁿ , où les a ⁱ et les b ⁱ sont des éléments de face=F9828 a et face=F9828 b respectivement, est encore un idéal, appelé produit des idéaux face=F9828 a et face=F9828 b et noté face=F9828 ab. Le produit ainsi défini est commutatif, associatif et admet un élément unité qui est l’anneau tout entier A = (1) (parfois appelé, pour cette raison, idéal unité). Si A est un anneau d’intégrité, le produit des deux idéaux non nuls (c’est-à-dire différents de0) est non nul et par suite l’ensemble M(A) des idéaux non nuls est un monoïde pour cette loi de composition; le monoïde M(A) jouera un rôle très important dans la troisième partie. Remarquons que si face=F9828 a = (a ) et face=F9828 b = (b ) sont principaux, alors on a face=F9828 ab = (ab ) et par suite l’application a(a ) est un homomorphisme du monoïde A dans le monoïde M(A) (l’image d’un produit est le produit des images, et l’élément d’unité a pour image l’élément unité).

Deux éléments a et b de A sont dits congrus modulo un idéal face=F9828 a, et on note:

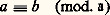si la différence a 漣 b appartient à face=F9828 a; dans le cas où face=F9828 a = (c ) est principal, on retrouve la notion usuelle de congruence modulo c . Considérons l’ensemble quotient, noté A/ face=F9828 a, de A par cette relation (c’est manifestement une relation d’équivalence). Si a 漣 et b 漣 sont les classes de a et b respectivement, on vérifie que a + b et ab sont indépendants des représentants a et b choisis et que les deux lois de composition ainsi définies font de A/ face=F9828 a un anneau commutatif unitaire appelé anneau quotient de A par l’idéal face=F9828 a. Dans le cas où A est l’anneau Z des entiers relatifs et face=F9828 a l’ensemble (n ) des multiples d’un entier n , cet anneau n’est autre que l’anneau des classes résiduelles d’entiers modulo n ^{[cf. ANNEAUX ET ALGÈBRES]}.

Un idéal face=F9828 p A est dit premier s’il ne contient le produit ab de deux éléments de A que lorsqu’il contient au moins l’un d’entre eux; dans l’anneau Z des entiers, cette condition caractérise les idéaux principaux (p ) engendrés par un nombre premier p . On voit facilement qu’un idéal est premier si, et seulement si, l’anneau quotient est sans diviseurs de zéro; ainsi, un exemple important d’idéaux premiers est constitué par les idéaux maximaux face=F9828 p (idéaux qui ne sont contenus dans aucun autre idéal propre) caractérisés par le fait que A/ face=F9828 p est un corps. Généralisons maintenant aux idéaux quelconques les propriétés des idéaux principaux de Z engendrés par les puissances des nombres premiers: un idéal face=F9828 q est dit primaire si ab 捻 face=F9828 q et a 殮 face=F9828 q entraînent qu’une puissance de b appartient à face=F9828 q; il résulte des définitions que si face=F9828 q est primaire, son radical , qui est l’ensemble des éléments dont une puissance appartient à face=F9828 q est premier. Nous verrons, dans la quatrième partie, l’importance des idéaux primaires.

Éléments entiers

Soit A un anneau d’intégrité contenu dans un corps K. On dit qu’un élément de K est entier sur A s’il est racine d’un polynôme:

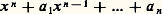à coefficients dans A et dont le coefficient dominant est égal à 1. Il est clair que tout élément de A est entier sur A puisqu’il est racine du polynôme x 漣 a ; on peut montrer que l’ensemble des éléments de K qui sont entiers sur A forme un anneau (qui contient donc A) appelé la fermeture intégrale de A dans K . Un cas particulièrement important est celui où K est le corps des fractions de A (cf. supra ); si les seuls éléments du corps des fractions de A qui sont entiers sur A sont les éléments de A, on dit que l’anneau A est intégralement clos . Ces anneaux jouent un rôle essentiel dans de nombreuses questions, en théorie des nombres et en géométrie algébrique notamment.

2. L’arithmétique élémentaire et les anneaux principaux

Un anneau principal est un anneau d’intégrité dans lequel tout idéal est principal, c’est-à-dire formé des multiples d’un même élément, appelé générateur de l’idéal. L’étude de la divisibilité dans un tel anneau est analogue à la théorie arithmétique élémentaire des nombres entiers, qui en constitue d’ailleurs un cas particulier. L’étude de la divisibilité dans l’anneau K [x ] des polynômes à une variable sur un corps K rentre aussi dans ce cadre.

Exemples

a ) Montrons que l’anneau Z des entiers relatifs est principal . La démonstration repose sur la propriété suivante de divisibilité dans cet anneau: étant donné deux entiers rationnels a et b , b 礪 0, il existe un couple et un seul d’entiers rationnels q et r tels que:

les nombres q et r s’appellent respectivement le quotient et le reste de la division de a par b . Soit donc maintenant face=F9828 a un idéal de Z. Si face=F9828 a =0, on a face=F9828 a = (0); sinon face=F9828 a contient des éléments strictement positifs puisque avec tout élément a il contient son opposé 漣 a = ( face=F0019 漣 1) a . Soit b le plus petit élément strictement positif de face=F9828 a; montrons que tout élément a de face=F9828 a est un multiple de b . En effet, l’existence de la division dans Z permet d’écrire a = bq + r , 0 諒 r 麗 b ; or le multiple bq de b appartient à face=F9828 a, donc aussi r = a 漣 bq : la définition de b entraîne r = 0.

b ) Un autre exemple important d’anneau principal est l’anneau K[X] des polynômes à coefficients dans un corps commutatif K. La démonstration repose ici encore sur l’existence dans cet anneau d’une division «euclidienne»: si A et B sont des polynômes, il existe un couple et un seul de polynômes Q et R tels que A = BQ + R, le degré de R étant strictement inférieur au degré de B. On montre alors, par une démonstration analogue à ce qui précède, qu’un idéal face=F9828 a 0 de K[X] est formé des multiples de tout polynôme B non nul de face=F9828 a dont le degré est le plus petit possible ^{[cf. POLYNÔMES]}.

c ) À propos de recherches sur les formes quadratiques, Gauss a utilisé le fait que l’anneau des nombres complexes de la forme a + bi , a , b 捻 Z (appelés entiers de Gauss), possède une arithmétique comparable à celle des entiers ordinaires. Ce fait s’explique, avec la terminologie ci-dessus, par le fait que cet anneau est principal.

Plus grand commun diviseur et plus petit commun multiple

Dans ce qui suit, nous nous limiterons, pour simplifier les notations, au cas de deux éléments, mais il est clair que tous les résultats s’étendent sans difficulté au cas d’un nombre fini d’éléments.

Soient x , y deux éléments d’un anneau principal A et considérons l’idéal (x , y ) constitué par les éléments de la forme ax + by , a , b 捻 A. Puisque A est principal, cet idéal est engendré par un élément d , déterminé à cela près qu’on peut le remplacer par ud , où u est un élément inversible quelconque de l’anneau. On appelle plus grand commun diviseur (en abrégé P.G.C.D.) de x et y tout élément d tel que (x , y ) = (d ).

Puisque d 捻 (d ), on voit en particulier qu’il existe a , b 捻 A tels que:

(ce résultat constitue le théorème de Bezout ). Justifions la terminologie adoptée en montrant qu’un élément z de A divise simultanément x et y si et seulement s’il divise d : puisque (d ) contient x et y , ces nombres sont des multiples de d et, par suite, tout diviseur de d divise x et y ; réciproquement, si z divise x et y , écrivons x = zx , y = zy , et portons dans (); on obtient d = z (ax + by ), ce qui prouve que z divise d . Dans le cas de l’anneau Z des entiers rationnels, d est déterminé au signe près puisque les seuls éléments inversibles sont ici + 1 et 漣 1; on peut donc prendre d 礪 0 et on retrouve la notion élémentaire de P.G.C.D. enseignée dans les classes primaires.

Deux éléments x et y de A sont dits premiers entre eux s’ils admettent 1 pour P.G.C.D., c’est-à-dire si leurs seuls diviseurs communs sont les unités de l’anneau. D’après le théorème de Bezout indiqué ci-dessus, x et y sont premiers entre eux si et seulement s’il existe des éléments a , b 捻 A tels que ax + by = 1 (la condition suffisante résulte du fait que, si cette relation est satisfaite, tout diviseur commun à x et y divise 1). Ce résultat entraîne facilement le théorème de Gauss (ou lemme d’Euclide ), qui s’énonce: «Soit x et y des éléments non nuls d’un anneau principal A et d un diviseur du produit xy ; si d et x sont premiers entre eux, alors d divise y .» En effet, puisque d et x sont premiers entre eux, il existe u , v 﨎 A tels que: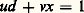

d’où après multiplication par y ,

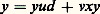puisque d divise xy et yud , il divise aussi y .

Soit encore x et y des éléments d’un anneau principal A. Les multiples de x et de y sont les éléments de (x ) et (y ) respectivement et par suite les multiples communs à x et y sont les éléments de l’idéal (x ) 惡 (y ). Puisque l’anneau A est principal, cet idéal est formé des multiples d’un élément défini à un facteur inversible près: on appelle plus petit commun multiple (en abrégé P.P.C.M.) de x et y tout élément m de A tel que (x ) 惡 (y ) = (m ); avec cette définition, tout multiple de x et y est un multiple de m .

Décomposition en facteurs premiers

Pour tout anneau d’intégrité, on a défini sous le titre 1 les éléments premiers. On peut montrer que les anneaux principaux possèdent les deux propriétés fondamentales (F¹) et (F²) suivantes.

(F¹) Décomposition en facteurs premiers . Tout élément x non nul et non inversible est produit d’un nombre fini d’éléments premiers (pas nécessairement distincts).

(F²) «Unicité» de la décomposition . Si

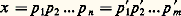sont deux décompositions d’un élément x comme produit d’éléments premiers, alors m = n , et, quitte à modifier éventuellement l’ordre des facteurs, les éléments p ⁱ et p ⁱ sont associés (c’est-à-dire p ⁱ = u ⁱ p ⁱ , u ⁱ inversible), pour i = 1,2,...,n .

Remarquons que, puisque deux éléments de A engendrent le même idéal si et seulement s’ils sont associés, les conditions (F¹) et (F²) expriment que tout idéal de A non nul et différent de A (de la forme (x ) puisque A est principal) s’écrit, de manière unique à l’ordre près des facteurs, comme un produits d’idéaux premiers:

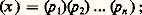ainsi la situation est plus simple dans le monoïde M(A) que dans le monoïde A puisqu’il n’y a plus cette fois d’ambiguïté quant au sens à donner à l’expression unicité de la décomposition . Dans la pratique, on élimine cette ambiguïté en choisissant une fois pour toutes un ensemble P d’éléments premiers de A tels que pour tout élément premier p de A il existe un élément premier p de P et un seul qui soit associé à p . Les propriétés (F¹) et (F²) s’expriment alors ainsi: tout élément x de A s’écrit, de manière unique à l’ordre près des facteurs, sous la forme:

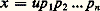où u est une unité de A et où les p ⁱ sont des éléments de P (pas nécessairement distincts). Ainsi, dans le cas de l’anneau Z des entiers relatifs, on peut prendre pour P l’ensemble des nombres premiers positifs, et tout entier relatif x s’écrit de manière unique sous la forme:

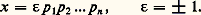Anneaux factoriels

De manière générale, on appelle anneau factoriel tout anneau d’intégrité possédant les propriétés (F¹) et (F²); remarquons d’ailleurs que l’on peut remplacer la condition (F²) par la condition suivante:

(F³) Si un élément premier de A divise un produit, il divise au moins un des facteurs de ce produit.

Les anneaux factoriels constituent une classe plus vaste que celle des anneaux principaux; cette classe possède la remarquable propriété de stabilité suivante: si A est un anneau factoriel, alors l’anneau A [X] des polynômes à coefficient dans A est lui aussi factoriel. On obtient ainsi, par récurrence, que l’anneau K[X¹,...,Xⁿ ] des polynômes à n variables sur un corps K est factoriel, alors qu’il n’est pas principal pour n 閭 2 (en effet, dans l’anneau K[X,Y] des polynômes à deux variables, l’idéal (X,Y), formé des polynômes de la forme XP(X,Y) + YQ(X,Y), n’est pas principal). L’anneau K[[X]] des séries formelles à coefficients dans un corps K est factoriel; mais, par contre, l’anneau A[[X]] peut ne pas être factoriel même si A est un anneau factoriel (contre-exemple dû à Samuel).

Pour terminer, signalons, en liaison avec la définition donnée plus haut, que tout anneau factoriel est intégralement clos . En effet, soit xy ^-1, x , y éléments de A, un élément du corps des fractions de A; on peut supposer que x et y n’ont pas de facteurs premiers communs. Si xy ^-1 est entier sur A, il est racine d’un polynôme à coefficients dans A dont le coefficient dominant est égal à 1, soit:

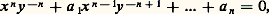a ⁱ 捻 A; on en déduit que:

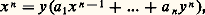c’est-à-dire que x ⁿ est un multiple de y . Mais si y n’est pas un élément inversible de A, on obtient une contradiction puisque, d’après (F³), tout diviseur premier de y doit alors diviser x .

3. Les anneaux de Dedekind et la théorie multiplicative des idéaux

L’extension de l’arithmétique classique aux anneaux d’entiers algébriques s’est longtemps heurtée au fait que ces anneaux ne sont pas factoriels. Par exemple, dans l’anneau Z[ 連漣 3] des nombres complexes de la forme a + ib 連3, a , b entiers relatifs, le nombre 4 admet les deux décompositions:

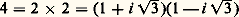en facteurs premiers non associés deux à deux et par suite cet anneau n’est pas factoriel. Dedekind, à partir des travaux de Kummer, mit en évidence que, pour un tel anneau A, la notion importante était celle d’idéal premier et non pas d’élément premier, comme pouvait le faire croire l’étude élémentaire des entiers relatifs. En somme, tout revient ici à remplacer l’étude du monoïde A des éléments non nuls de A par celle du monoïde M(A) des idéaux non nuls de A; on trouve l’unicité de la décomposition en facteurs premiers «idéaux». Chaque élément a non inversible de A étant identifié à l’idéal principal (a ) qu’il engendre peut ainsi s’écrire, de manière unique, comme un produit d’idéaux premiers.

La définition abstraite des anneaux de Dedekind que nous formulons ici a été donnée pour la première fois, en 1927, par la mathématicienne allemande Emmy Noether.

Anneaux de Dedekind

Par définition, on appelle anneau de Dedekind tout anneau intégralement clos et noethérien (c’est-à-dire dans lequel tout idéal est engendré par un nombre fini d’éléments, cf. infra ) dans lequel tout idéal premier non nul est maximal. Cela signifie que le quotient de A par un idéal premier non nul quelconque est non seulement un anneau d’intégrité mais même un corps.

L’exemple le plus simple d’un tel anneau est l’anneau Z [ 連d ] des nombres de la forme a + b 連d , a , b entiers relatifs, d entier tel que d 令 2 ou 3 (mod. 4). Plus généralement, Dedekind a démontré que, si K est une extension finie du corps Q des nombres rationnels (K est appelé un corps de nombres algébriques), alors la fermeture intégrale A de l’anneau Z dans K est un anneau de Dedekind (A est appelé l’anneau des entiers du corps K; cf. théorie des NOMBRES Nombres algébriques). En fait, l’exemple précédent, qui est très important en théorie des nombres, est lui-même un cas particulier du résultat algébrique suivant: soit A un anneau de Dedekind, de corps des quotients K, et soit L une extension finie de K (cf. CORPS [mathématiques]); alors la fermeture intégrale de A dans L est un anneau de Dedekind.

L’intérêt essentiel des anneaux de Dedekind réside dans la structure particulièrement simple, pour un tel anneau, du monoïde M(A) des idéaux non nuls. On a le résultat suivant: un anneau d’intégrité A est un anneau de Dedekind si, et seulement si, tout idéal non nul de A s’écrit de manière unique (à l’ordre près des facteurs) comme produit d’idéaux premiers non nuls. Soit face=F9828 a un tel idéal non nul; écrivant face=F9828 pa si l’idéal premier face=F9828 p figure a fois dans la décomposition de face=F9828 a, on peut donc écrire face=F9828 a de manière unique sous la forme:

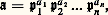les face=F9828 pⁱ étant des idéaux premiers distincts . Désignant par P l’ensemble des idéaux premiers non nuls de A, on écrit souvent cette décomposition sous la forme:

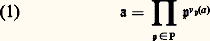en convenant que v face=F9828 size=1^p(face=F9828 a) = 0 quand l’idéal premier face=F9828 p ne figure pas dans la décomposition de face=F9828 a; par définition le produit ci-dessus est alors égal au produit fini correspondant aux idéaux tels que v face=F9828 size=1^p(face=F9828 a) 礪 0. L’intérêt de cette convention réside dans des formules du type suivant: si face=F9828 a et face=F9828 b sont deux idéaux, alors on a:

c’est-à-dire, avec les notations ci-dessus, v face=F9828 size=1^p(face=F9828 ab) = v face=F9828 size=1^p(face=F9828 a) + v face=F9828 size=1^p(face=F9828 b).

Remarquons que l’existence et l’unicité de la décomposition de tout idéal de M(A) comme produit d’idéaux premiers permet d’appliquer à M(A) tous les résultats élémentaires relatifs à la divisibilité des entiers; par exemple si face=F9828 a et face=F9828 b sont deux idéaux non nuls, leurs diviseurs communs, ou leurs multiples communs, sont les diviseurs, ou les multiples, d’éléments appelés respectivement le P.G.C.D. et le P.P.C.M. de face=F9828 a et face=F9828 b et qui s’écrivent: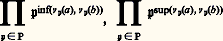

respectivement.

Idéaux fractionnaires

Soit A un anneau d’intégrité; la structure du monoïde M(A) des idéaux non nuls donne des indications sur la structure du monoïde multiplicatif A. De la même manière, pour étudier la structure du groupe multiplicatif K du corps des quotients K de A, on est amené à étendre la notion d’idéal.

Un sous-ensemble face=F9828 a, non réduit à0, de K est appelé un idéal fractionnaire si c’est un sous-anneau de K stable par multiplication par les éléments de A et pour lequel il existe un élément d 0 de A tel que dx appartienne à A pour tout x de face=F9828 a; cette définition revient à dire qu’un idéal fractionnaire est l’ensemble des produits d ^{- 1}y , d non nul fixé, lorsque y parcourt un idéal (au sens usuel) de A. Il est clair qu’un idéal non nul est un idéal fractionnaire; dans la théorie des idéaux fractionnaires, on appelle souvent idéaux entiers les idéaux usuels pour éviter toute confusion.

Il est facile de généraliser aux idéaux fractionnaires les opérations usuelles sur les idéaux: en particulier, si face=F9828 a et face=F9828 b sont des idéaux fractionnaires, on vérifie que l’ensemble des sommes finies d’éléments du type xy , x dans face=F9828 a et y dans face=F9828 b, est un nouvel idéal fractionnaire appelé le produit de face=F9828 a et face=F9828 b noté face=F9828 ab; l’ensemble I(A) des idéaux fractionnaires non nuls est ainsi un monoïde pour cette multiplication. Un idéal fractionnaire face=F9828 a est dit inversible s’il existe un idéal fractionnaire face=F9828 b tel que face=F9828 ab = A. Avec cette terminologie, on peut maintenant donner une nouvelle définition des anneaux de Dedekind: «Un anneau de Dedekind est un anneau d’intégrité tel que tout idéal fractionnaire non nul est inversible.» Le monoïde I(A) des idéaux fractionnaires non nuls est alors un groupe multiplicatif et tout élément de ce groupe peut s’écrire, de manière unique à l’ordre des facteurs près, sous la forme:

où les v face=F9828 size=1^p(face=F9828 a) sont des entiers relatifs , nuls sauf pour un nombre fini d’idéaux premiers. Dans cette décomposition, les idéaux entiers sont caractérisés par le fait que v face=F9828 size=1^p(face=F9828 a) 閭 0 pour tout idéal premier non nul.

Valuations et idéaux premiers

Soit A un anneau de Dedekind. Pour tout élément a 0 de A, l’idéal principal (a ) a une décomposition du type (1): posons, par définition, v face=F9828 size=1^p(a) = v face=F9828 size=1^p((a)) et étendons cette fonction au corps K des fractions de A en posant: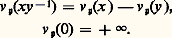

On vérifie que, pour z = xy ^-1 dans K, la valeur ainsi définie est indépendante de la décomposition xy ^-1 choisie; le nombre v face=F9828 size=1^p(z ) ainsi défini n’est autre que l’exposant de face=F9828 p dans la décomposition (2) de l’idéal fractionnaire (z ) (formé des éléments az pour a parcourant A). On obtient ainsi une valuation (discrète normée) sur K, c’est-à-dire une fonction v définie sur K et à valeurs dans Z 聆+ 秊參 telle que:(a ) pour z parcourant K, v (z ) parcourt l’ensemble Z des entiers relatifs et v (0) = + 秊;

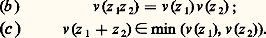Ainsi, à tout idéal premier face=F9828 p non nul, on a fait correspondre une valuation, dite essentielle ; par définition, une telle valuation prend des valeurs positives ou nulle sur tout élément de A. Réciproquement, on peut montrer que toute valuation (au sens cidessus) positive sur A est obtenue à partir d’un idéal premier; il existe ainsi une correspondance biunivoque entre les valuations (discrètes normées) positives sur A et les idéaux premiers non nuls de l’anneau A. Un exemple est donné par l’anneau Z des entiers relatifs et l’anneau Z^p des nombres p -adiques (cf. théorie des NOMBRES – Nombres p -adiques).

4. Anneaux noethériens

Avant Hilbert, les mathématiciens connaissaient fort peu de résultats sur les anneaux de polynômes à plusieurs variables. À propos de recherches sur la théorie des invariants, Hilbert mit en évidence le fait que tout idéal d’un tel anneau est engendré par un nombre fini d’éléments et montra tout le parti que l’on pouvait tirer de cette propriété; par là même, il dégageait l’importance des anneaux avec conditions de finitude qui allaient être étudiés systématiquement sous forme générale par E. Noether. Signalons que les conditions de finitude en un sens plus large jouent un rôle absolument essentiel dans toutes les recherches «géométriques» contemporaines en géométrie algébrique ou analytique (au sens moderne, à savoir l’étude des espaces analytiques) et dans de nombreuses questions d’algèbre homologique.

Définitions équivalentes

Un anneau noethérien est un anneau commutatif unitaire A qui vérifie une des trois conditions de finitude équivalentes suivantes:

Condition (a ), dite de chaîne ascendante: «Toute suite strictement croissante d’idéaux est finie», ou encore : «Si :

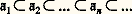est une suite infinie d’idéaux de A encastrés, il existe un entier n tel que face=F9828 an = face=F9828 an 漣 1 = ...».

Condition (b ) : «Toute famille non vide d’idéaux a un élément maximal», ce qui signifie que si (face=F9828 aⁱ )ⁱ size=1^{捻 I}, I non vide fini ou non, est une famille d’idéaux de A, il existe un indice i⁰ pour lequel l’idéal face=F9828 aⁱ⁰ n’est contenu strictement dans aucun autre idéal de la famille.

Condition (c ): «Tout idéal est engendré par un nombre fini d’éléments», c’est-à-dire que si face=F9828 a est un idéal de A, il existe des éléments x ¹, ..., x ⁿ , en nombre fini, tels que face=F9828 a soit l’ensemble des éléments de la forme a ¹x ¹ + ... + a ⁿx ⁿ lorsque a ¹, ..., a ⁿ parcourent A indépendamment l’un de l’autre.

Esquissons la démonstration de l’équivalence de ces trois conditions car elle est instructive. Pour montrer que (a ) entraîne (b ), on raisonne par l’absurde. Si la famille (face=F9828 aⁱ )ⁱ size=1^{捻 I} n’admettait pas d’élément maximal, alors pour tout i size=1^{捻 I} on pourrait trouver j 捻 I tel que l’idéal face=F9828 a^j contienne strictement l’idéal face=F9828 aⁱ et on pourrait construire ainsi, par récurrence à partir d’un idéal face=F9828 aⁱ , une suite infinie strictement croissante d’idéaux.

Montrons que (b) entraîne (c). Soit face=F9828 a un idéal et considérons la famille des idéaux de type fini (c’est-à-dire engendré par un nombre fini d’éléments) contenus dans face=F9828 a; cette famille est non vide car elle contient0 et par suite elle admet un élément maximal face=F9828 b engendré par des éléments x ¹, ..., x ⁿ. Pour tout x de face=F9828 b, l’idéal engendré par les éléments x ¹, ..., x ⁿ, x contient face=F9828 b, appartient à la famille d’idéaux considérée et par suite est égal à face=F9828 b puisque face=F9828 b est maximal. Ainsi face=F9828 a = (x ¹, ..., x ⁿ).

Pour terminer, montrons que (c ) entraîne (a). Soit face=F9828 aⁿ une suite croissante d’idéaux encastrés. On varifie que, dans ce cas, la réunion des idéaux face=F9828 an est encore un idéal; d’après (c ), cet idéal est engendré par un nombre fini d’éléments x ¹, ..., x ⁿ et, par définition d’une réunion, il existe des entiers p ¹, ..., p ⁿ tels que x ¹ 捻 face=F9828 ap¹, ..., x n 捻 face=F9828 apⁿ . Il est maintenant clair que, si p est le plus grand des entiers p ¹, ..., p ⁿ, on a face=F9828 ak = face=F9828 a pour k 閭 p .

Exemples d’anneaux noethériens

Par définition, les anneaux de Dedekind, et en particulier, bien entendu, les anneaux principaux, sont des anneaux noethériens. Une source importante d’exemples ne rentrant pas dans les précédents est la remarquable propriété de stabilité suivante, découverte par Hilbert: si A est un anneau noethérien, l’anneau A [X] des polynômes à coefficients dans A est lui aussi noethérien; par récurrence, ce résultat s’étend à l’anneau A[X¹, ..., Xⁿ ] des polynômes à n variables sur un anneau noethérien A. On obtient ainsi que l’anneau des polynômes à n variables à coefficients dans un corps K est noethérien, alors que cet anneau n’est ni principal, ni même de Dedekind, pour n 閭 2. Signalons que le théorème de Hilbert s’étend à l’anneau A[X¹, ..., Xⁿ ] des séries formelles à coefficients dans un anneau noethérien A; dans le même ordre d’idées, si K est le corps des nombres réels ou des nombres complexes, l’anneau KX¹, ..., Xⁿ des séries convergentes est noethérien ^{[cf. ANNEAUX ET ALGÈBRES]}.

Décomposition primaire

Remarquons que, pour un anneau commutatif avec unité, les opérations d’intersection et de produit de deux idéaux jouent des rôles assez semblables. Dans le cas des anneaux principaux par exemple, si p et q sont deux éléments premiers, alors (p ) (q ) = (p ) 惡 (q ) et par suite la décomposition d’un idéal en idéaux premiers peut s’écrire indifféremment:

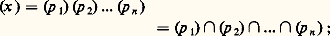cette situation est d’ailleurs la même pour un anneau de Dedekind quelconque. Dans le cas d’un anneau noethérien, le monoïde multiplicatif M(A) n’est guère utilisable, mais on peut donner un théorème de décomposition de tout idéal comme intersection d’idéaux d’un type plus général que les idéaux premiers, les idéaux primaires (cf. supra ).

Le théorème de décomposition de Lasker-Noether affirme que tout idéal d’un anneau nœthérien s’écrit sous la forme :

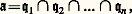où les face=F9828 qⁱ sont des idéaux primaires auxquels on peut imposer les deux conditions suivantes; aucun des idéaux face=F9828 qⁱ ne contient l’intersection des autres et les radicaux face=F9828 pⁱ des idéaux face=F9828 qⁱ sont des idéaux premiers distincts (cf. supra , chap. 1). Il n’y a pas unicité pour une telle décomposition, mais les idéaux premiers face=F9828 pⁱ définis ci-dessus sont déterminés de manière unique et appelés les idéaux premiers de l’idéal face=F9828 a. Parmi ces idéaux premiers, ceux qui sont minimaux, c’est-à-dire qui ne contiennent aucun des autres sont dits isolés et ont une grande importance en géométrie algébrique. Cette terminologie est justifiée par le fait que, dans le cas où face=F9828 a est un idéal de l’anneau K[x ¹, ..., x ⁿ ] des polynômes à n variables sur un corps K, ces idéaux isolés correspondent aux composantes irréductibles de l’ensemble des points Kⁿ où s’annulent simultanément tous les polynômes de l’idéal ^{[cf. GÉOMÉTRIE ALGÉBRIQUE]}.

Encyclopédie Universelle. 2012.